Answer:
0.28 yr
Explanation:
To find the doubling time with continuous compounding, we should look at the formula:
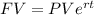
FV = future value, and
PV = present value
If FV is twice the PV, we can calculate the doubling time, t
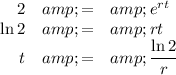
1. Samuel's doubling time
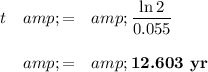
2. Claire's doubling time

3. Samuel's doubling time vs Claire's
12.603 - 12.323 = 0.28 yr
It would take 0.28 yr longer for Samuel's money to double than Claire's.