Question

100 POINTS, NEED HELP ASAP

i just don’t get how to calculate all of these things

Answer 1

a) 57.4 N

b) 31 m/s²

c) 1.97 s

d) 13.7 N

e) 68.6 N

Step-by-step explanation:

Hope that helped!

Answer 2

a) 57.4 N

b)
`3.1 m/s^2`

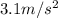
c) 1.97 s

d) 13.7 N

e) 68.6 N

Step-by-step explanation:

The text and some of the data in the problem are missing, so I will make some assumptions on the problem and on some values.

a)

Here there are two girls that are applying each a horizontal force of 30 N through two ropes on the sled, at an angle of
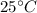`25^(\circ)C` from each other.

Here we want to find the net tension force: therefore, we have to resolve the two forces along two perpendicular directions, and calculate the resultant.

Calling the two forces
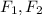`F_1,F_2` , and choosing the directions parallel and perpendicular to F1, we have:

- Along direction parallel to F1:

`F_(1x)=30N\\F_(2x)=(30)(cos 30^(\circ))=26.0 N`

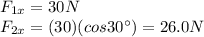
- Along the direction perpendicular to F1:

`F_(1y)=0\\F_(2y)=(30)(sin 25^(\circ))=12.7 N`

Therefore, the components of the net force are

`F_x=F_(1x)+F_(2x)=30+26.0=56.0 N\\F_y=F_(1y)+F_(2y)=0+12.7=12.7 N`

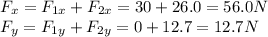
Therefore, the net tension force is:

`T=√(F_x^2+F_y^2)=√(56.0^2+12.7^2)=57.4 N`

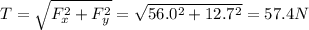
b)

The acceleration of the sled can be found by using Newton's second law of motion:

`\sum F = ma`

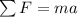
where

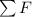`\sum F` is the net force on the sled

m = 14 kg is the mass of the sled

a is the acceleration

The net force on the sled is given by the difference between the tension force T (forward) and the frictional force
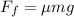`F_f=\mu mg` (backward), so we can write

`T-\mu mg = ma`

where:

T = 57.4 N is the net tension

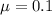`\mu=0.1` is the coefficient of friction

`g=9.8 m/s^2` is the acceleration due to gravity

Solving for the acceleration,

`a=(T-\mu mg)/(m)=(57.4-(0.1)(14)(9.8))/(14)=3.1 m/s^2`

c)

The motion of the sled is a uniformly accelerated motion, so we can use the following suvat equation:

`s=ut+(1)/(2)at^2`

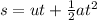
where

u is the initial velocity

t is the time

a is the acceleration

s is the displacement

In this problem, we have:

u = 0 (I assume the sled starts from rest)

s = 6.0 m (distance covered by the sled)

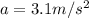`a=3.1 m/s^2` (acceleration)

Solving for t, we find the time needed:

`t=\sqrt{(2s)/(a)}=\sqrt{(2(6.0))/(3.1)}=1.97 s`

d)

The force of kinetic friction on a moving object on a flat surface is given by

`F_f = \mu mg`

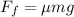
where

`\mu` is the coefficient of kinetic friction

m is the mass of the object

g is the acceleration due to gravity

For the sled in this problem, we have:

`\mu=0.1`

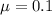
m = 14 kg

`g=9.8 m/s^2`

Therefore, the force of kinetic friction is:

`F_f=(0.1)(14)(9.8)=13.7 N`

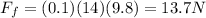
e)

Here the sled stops on a slope with angle of

`\theta=30^(\circ)`

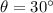
above the horizontal (I assumed this value since it is not given).

When the sled stops, there are two forces acting on it along the direction parallel to the slope:

- The component of the weight of the sled along the slope, down along the slope, of magnitude
`mg sin \theta`

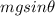
- The force of static friction,
`F_f`, up along the slope

The sled at this moment is in equilbrium, so the two forces are balanced; so we can write:

`F_f = mg sin \theta`

And by substituting

`m=14 kg`

`g=9.8 m/s^2`

We find:

`F_f=(14)(9.8)(sin 30^(\circ))=68.6 N`

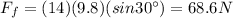
Note: if some of the values that I have assumed are different, you can just plug in the correct numbers into the equation and find other results, but the procedure remains the same.