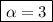1 Answer

Ryan Thames · Answer 1 · 2021-02-19T07:18:57+0000

Answer:

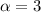
$\alpha=3$

Explanation:

Equation of a Circle

A circle of radius r and centered on the point (h,k) can be expressed by the equation

(x-h)^2+(y-k)^2=r^2

We are given the equation of a circle as

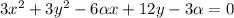
$3x^2+3y^2-6\alpha x+12y-3\alpha=0$

Note we have corrected it by adding the square to the y. Simplify by 3

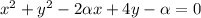
$x^2+y^2-2\alpha x+4y-\alpha=0$

Complete squares and rearrange:

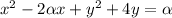
$x^2-2\alpha x+y^2+4y=\alpha$

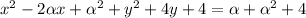
$x^2-2\alpha x+\alpha^2+y^2+4y+4=\alpha+\alpha^2+4$

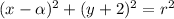
$(x-\alpha)^2+(y+2)^2=r^2$

We can see that, if r=4, then

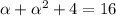
$\alpha+\alpha^2+4=16$

Or, equivalently

$\alpha^2+\alpha-12=0$

There are two solutions for
$\alpha$ :

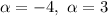
$\alpha=-4,\ \alpha=3$

Keeping the positive solution, as required:

$\boxed{\alpha=3}$

Please log in or register to add a comment.