Question

Marquise has 200200200 meters of fencing to build a rectangular garden.

The garden's area (in square meters) as a function of the garden's width www (in meters) is modeled by:
A(w)=-w^2+100wA(w)=−w
2
+100wA, left parenthesis, w, right parenthesis, equals, minus, w, squared, plus, 100, w
What side width will produce the maximum garden area?

Answer 1

50 took khan test

Explanation:

Answer 2

The side width that produce the maximum area will be 50 meters

Explanation:

The correct question is

Marquise has 200 meters of fencing to build a rectangular garden. The garden's area (in square meters) as a function of the garden's width w (in meters) is modeled by: A ( w ) = − w 2 + 1 0 0 w. What side width will produce the maximum garden area?

we have

`A(w)=-w^2+100w`

where

A(w) ---> represent the garden's area in square meters

w ----> represent the garden width in meters

we know that

The given quadratic equation represent a vertical parabola open downward (the leading coefficient is negative)

The vertex represent a maximum

so

The x-coordinate of the vertex represent the width of the garden for the maximum area

The y-coordinate of the vertex represent the maximum area of the garden

Convert the quadratic equation into vertex form

`A(w)=-w^2+100w`

Factor the leading coefficient -1

`A(w)=-(w^2-100w)`

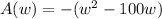
Complete the square

`A(w)=-(w^2-100w+50^2)+50^2`

`A(w)=-(w^2-100w+2,500)+2,500`

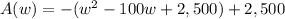
Rewrite as perfect squares

`A(w)=-(w-50)^2+2,500` ----> equation in vertex form

The vertex is the point (50,2,500)

Therefore

The maximum area of the garden is 2,500 square meters

The side width that produce the maximum area will be 50 meters (x-coordinate of the vertex)