Question

Given: AKLM is a trapezoid, AK=13 LM=14, KL=5, AM=20 Find: h

Answer 1

The height of the trapezoid is
`h=11.2`

Step-by-step explanation:

AKLM is a trapezoid.

The measurements of the trapezoid are AK=13, LM=14, KL=5, AM=20

We need to find the height of the trapezoid.

Let M' be a point on AM that is 5 units toward point A from M.

Let B be a point on AM such that KB⊥AM. Let x = AB; then BM' = 15 -x.

Using Pythagorean theorem, we have,

`x^(2)+h^(2)=13^(2)` --------(1)

`(15-x)^(2)+h^(2)=14^(2)`

`225-30x+x^(2) +h^(2)=14^(2)`-----------(2)

Subtracting the two equations, we have,

`\left(225-30 x+x^(2)+h^(2)\right)-\left(x^(2)+h^(2)\right)=196-169`

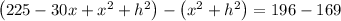
Simplifying, we get,

`225-30x=27`

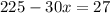
Subtracting both sides of the equation by 225, we get,

`30x=198`

Dividing by 30, we get,

`x=6.6`

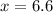
Substituting
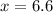`x=6.6` in the equation
`x^(2)+h^(2)=13^(2)`, we get,

`(6.6)^(2)+h^(2)=169`

`43.56+h^2=169`

`h=√(125.44)`

`h=11.2`

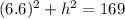
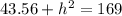
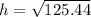
Thus, the height of the trapezoid is
`h=11.2`