Question

find the equation of the pair of lines perpendicular to the lines pair represented by the equation ax^2-2hxy+by^2=0 and passing through the origin.​

Answer 1

The equation of the pair of lines perpendicular to the lines given equation is
`b x^(2)-2 h x y+a y^(2)=0`.

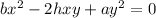Solution:

Given equation is
`a x^(2)+2 h x y+b y^(2)=0`.

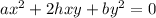Let
`m_1` and
`m_2` be the slopes of the given lines.

Sum of the roots =
`-\frac{\text {coefficient of } x y}{\text {coefficient of } y^(2)}`

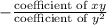
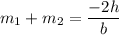`$m_1+m_2=(-2h)/(b)` – – – – – (1)

Product of the roots =
`-\frac{\text {coefficient of } x^2}{\text {coefficient of } y^(2)}`

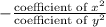
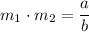`$m_1 \cdot m_2=(a)/(b)` – – – – – (2)

The required lines are perpendicular to these lines.

Slopes of the required lines are
`$-(1)/(m_(1)) \text { and }-(1)/(m_(2))`

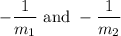
Required lines also passes through the origin,

therefore their y-intercepts are 0.

Hence their equations are:

`$y=-(1)/(m_(1))x \text { and }y=-(1)/(m_(2))x`

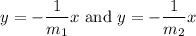
Do cross multiplication, we get

`m_1y=-x \ \text{and} \ m_2y=-x`

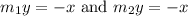
Add x on both sides of the equation, we get

`x+m_1y=0 \ \text{and} \ x+m_2y=0`

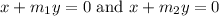
Therefore, the joint equation of the line is

`\left(x+m_(1) y\right)\left(x+m_(2) y\right)=0`

`x^2+m_2xy+m_1xy+m_1m_2y^2=0`

`x^(2)+\left(m_(1)+m_(2)\right) x y+m_(1) m_(2) y^(2)=0`

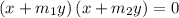
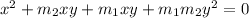
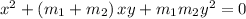
Substitute (1) and (2), we get

`$x^(2)+\left((-2 h)/(b)\right) x y+\left((a)/(b)\right) y^(2)=0`

To make the denominator same, multiply and divide first term by b.

`$ (b)/(b) x^(2)+\left((-2 h)/(b)\right) x y+\left((a)/(b)\right) y^(2)=0`

`$(bx^2-2hxy+ay^2)/(b) = 0`

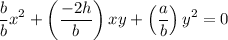
Do cross multiplication, we get

`b x^(2)-2 h x y+a y^(2)=0`

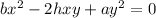
Hence equation of the pair of lines perpendicular to the lines given equation is
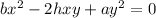`b x^(2)-2 h x y+a y^(2)=0`.