Question

Suppose that the Earth were moved to a distance of 0.25 AU from the Sun. How much

stronger or weaker would the Sun's gravitational pull on the Earth? Explain.

Answer 1

It increases by 16 times

Step-by-step explanation:

The magnitude of the gravitational force between two objects is given by the equation

`F=(Gm_1 m_2)/(r^2)`

where

G is the gravitational constant

m1, m2 are the masses of the two objects

r is their separation

In this problem, we call:

`m_1 = m` is the Earth's mass

`m_2 = M` is the Sun's mass

`r=1AU` is the initial distance Earth-Sun

So the gravitational force between the two objects is

`F=(GMm)/(r^2)`

Later, the Earth is moved to a distance of

r' = 0.25 AU

which is equivalent to write

`r'=(1)/(4)r`

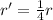
from the Sun.

Therefore, the new gravitational force will be:

`F'=(GMm)/(r'^2)=(GMm)/(((1)/(4)r)^2)=16((GMm)/(r^2))=16F`

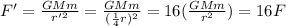
So, the gravitational force increases by a factor of 16.