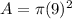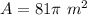A building engineer analyzes a concrete column with a circular cross section. The circumference of the column is 18 \pi18π18, pi meters. What is the area AAA of the cross sectio…

Question

asked Mar 23, 2021 170k views

1 Answer

Smart · Answer 1 · 2021-03-30T13:53:17+0000

Answer:

$A=81\pi\ m^2$

Explanation:

step 1

Find the radius of the circular cross section

The circumference is given by the formula

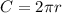
$C=2\pi r$

we have

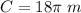
$C=18 \pi\ m$

substitute

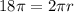
$18 \pi=2\pi r$

solve for r

simplify

$r=9\ m$

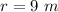
step 2

Find the area if the cross section of the column

The area of the cross section is equal to the area of a circle

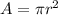
$A=\pi r^(2)$

we have

$r=9\ m$

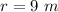
substitute

$A=\pi (9)^(2)$

$A=81\pi\ m^2$