Question

Each graph or table shows a linear relationship find slope

Answer 1

The slopes for the given data are.

4. Slope =
`(3)/(5)` = 0.6,

5. Slope =
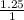`(1.25)/(1)` = 1.25, and

6. Slope =
`(3)/(4)` = 0.75.

Step-by-step explanation:

• The slope of a given line is determined by dividing the difference in y values of two particular coordinates by the difference in x values for the same two coordinates. Slope =
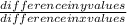  `(differenceinyvalues)/(differenceinxvalues)` (for the same two points).
• Slope for points (2, -2) and (-3, -5) is calculated the following method; Slope =
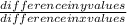  `(differenceinyvalues)/(differenceinxvalues)`, the difference in y values is 5 - 2 = 3 (since both values are in the same quadrant values are taken as positive) and the difference in x values is 2 - (-3) = 2 + 3 = 5. Slope =
  `(differenceinyvalues)/(differenceinxvalues)` =
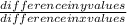  `(3)/(5)` = 0.6.

• Slope for any of the given points (2, 5) and (4, 7.5) is calculated the following method; Slope =
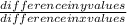  `(differenceinyvalues)/(differenceinxvalues)`, the difference in y values is 7.5 - 5 = 2.5 and the difference in x values is 4 - 2 = 2. Slope =
  `(differenceinyvalues)/(differenceinxvalues)` =
  `(2.5)/(2)` =
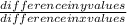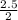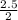  `(2.5)/(2)` = 1.25. The slope will be the same for all given coordinates.

• Slope for points (-2, 4) and (2, 1) is calculated the following method; Slope =
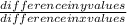  `(differenceinyvalues)/(differenceinxvalues)`, the difference in y values is 4 - 1 = 3 and the difference in x values is 2 - (-2) = 2 + 2 = 4. Slope =
  `(differenceinyvalues)/(differenceinxvalues)` =
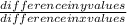  `(3)/(4)` = 0.75.