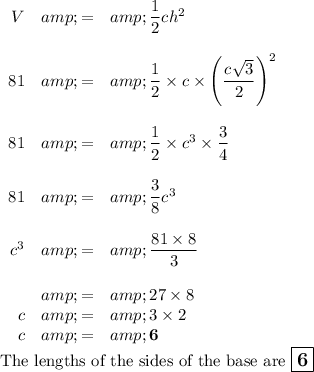Answer:

Explanation:
The formula for the volume of a right triangular prism is
V = ½ach, where
a = the height of the base
c = the length of a side of the base, and
h = the height of the prism
In your prism, a = h, so
V = ½ch²
The base is an equilateral, so
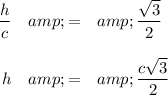
Then