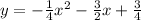What is the standard form given the vertex (-3,3) and the focus point (-3,2)

Question

asked Jan 3, 2021 213k views

1 Answer

Mic Fung · Answer 1 · 2021-01-09T22:52:18+0000

Answer:

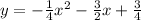
y=-(1)/(4)x^2-(3)/(2)x+(3)/(4)

Explanation:

The standard form of a parabola is written as

y=ax^2+bx+c

where a, b and c are the coefficients of the second-degree, first degree and zero-degree terms.

The coordinates of the vertex of a parabola is given by:

x_b = -(b)/(2a)

y_b=c-(b^2)/(4a)

The coordinates of the focus instead are given by

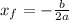
x_f=-(b)/(2a)

y_f=y_b+(1)/(4a)

In this problem, we know the coordinates of the vertex and of the focus point:

Vertex: (-3,3)

Focus point: (-3,2)

So we have:

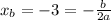x_b=-3=-(b)/(2a) (1)

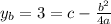y_b=3=c-(b^2)/(4a) (2)

y_f=2=y_b+(1)/(4a) (3)

From eq.(1) we get

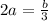2a=(b)/(3) (4)

Substituting into (2),

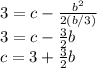$3=c-(b^2)/(2(b/3))\\3=c-(3)/(2)b\\c=3+(3)/(2)b$ (5)

Now rewriting eq.(3) as

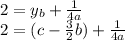
$2=y_b+(1)/(4a)\\2=(c-(3)/(2)b)+(1)/(4a)$

And substituting (4) and (5) into this, we can find b:

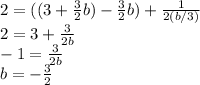
$2=((3+(3)/(2)b)-(3)/(2)b)+(1)/(2(b/3))\\2=3+(3)/(2b)\\-1=(3)/(2b)\\b=-(3)/(2)$

Then we can find a and c:

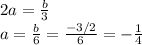
$2a=(b)/(3)\\a=(b)/(6)=(-3/2)/(6)=-(1)/(4)$

And

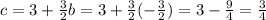
c=3+(3)/(2)b=3+(3)/(2)(-(3)/(2))=3-(9)/(4)=(3)/(4)

So the parabola is

y=-(1)/(4)x^2-(3)/(2)x+(3)/(4)