Question

Determine between which consecutive integers the real zeros

Answer 1

The question is related to determining the real zeros of a function graphically, but the function's equation or graph is not provided. In statistics, the term 'real zeros' might pertain to z-scores, but in this context, real zeros are the x-values where a function's graph intersects the x-axis. Additionally, information about significant figures of zeros in a number has been provided, differentiating between left-end zeros (never significant) and right-end zeros (significance depends on decimal point presence).

Step-by-step explanation:

The student's question seems to be asking for help in determining between which consecutive integers the real zeros of a function are located. Unfortunately, the question does not provide the actual function or its graph. From the information provided, we know that when a real zero of a function is graphically determined, one might need to zoom in on the graph to see between which integers on the x-axis the zero occurs. To find the real zeros graphically, you would look for where the graph crosses or touches the x-axis, which indicates that the y-value (or the function's output) is zero at that point.

In a different context, figuring out the real zeros can be associated with the standard normal distribution, where the variable 'z' represents the z-score. In this case, the real zeros would be the values of 'x' for which the areas under the standard normal curve equal zero, but normally z-scores don't correspond to the concept of zeros of a function.

In terms of significant figures, the zeros in a given number can either be significant or not, depending on their position and whether the number includes a decimal point. For example, left-end zeros are never significant, while right-end zeros may or may not be significant based on the presence of a decimal point.

Answer 2

Option B:
`-1<x<0` is the interval in which
`f(x)` has a real zero

Step-by-step explanation:

The given equation is
`f(x)=3 x^(3)-5 x^(2)+5 x+7`

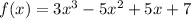
We need to determine x at which the value of f(x) becomes zero.

Option A:
`-1<x<0 ; 0<x<1 ; 1<x<2 ; 2<x<3`

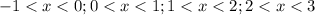
Let us substitute the values of x in the equation f(x), we get,

(i) Consider the 1st interval
`-1<x<0`

`f(-1)=3 (-1)-5 (1)+5(-1)+7=-6`

`f(0)=3 (0)-5 (0)+5(0)+7=7`

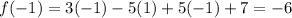
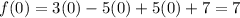
Since, there is a change of sign between the two interval, f(x) has a zero between the interval
`-1<x<0`

(ii) Consider the 2nd interval
`0<x<1`

`f(0)=3 (0)-5 (0)+5(0)+7=7`

`f(1)=3 (1)-5 (1)+5(1)+7=10`

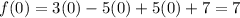
Since, there is no change of sign between the two interval, f(x) does not have a zero between the interval
`0<x<1`

(iii) Consider the 3rd interval
`1<x<2`

`f(1)=3 (1)-5 (1)+5(1)+7=10`

`f(2)=3 (8)-5 (4)+5(2)+7=21`

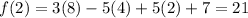
Since, there is no change of sign between the two interval, f(x) does not have a zero between the interval
`1<x<2`

(iv) Consider the 4th interval
`2<x<3`

`f(2)=3 (8)-5 (4)+5(2)+7=21`

`f(3)=3 (27)-5 (9)+5(3)+7=58`

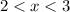
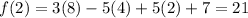
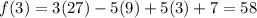
Since, there is no change of sign between the two interval, f(x) does not have a zero between the interval
`2<x<3`

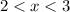
From all the above 4 options, there is no change of sign between the intervals and hence, Option A is not the correct answer.

Option B:
`-1<x<0`

Let us substitute the values of x in the equation f(x), we get,

`f(-1)=3 (-1)-5 (1)+5(-1)+7=-6`

`f(0)=3 (0)-5 (0)+5(0)+7=7`

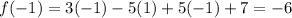
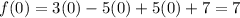
Since, there is a change of sign between the two interval, f(x) has a zero between the interval
`-1<x<0`

Hence, Option B is the correct answer.

Option C:
`1<x<2`

Let us substitute the values of x in the equation f(x), we get,

`f(1)=3 (1)-5 (1)+5(1)+7=10`

`f(2)=3 (8)-5 (4)+5(2)+7=21`

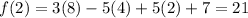
Since, there is no change of sign between the two interval, f(x) does not have a zero between the interval
`1<x<2`

Hence, Option C is not the correct answer.

Option D:
`-8<x<-7`

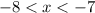
Let us substitute the values of x in the equation f(x), we get,

`f(-8)=3 (-512)-5 (64)+5(-8)+7=-1889`

`f(-7)=3 (-343)-5 (49)+5(-7)+7=-1302`

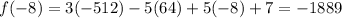
Since, there is no change of sign between the two interval, f(x) does not have a zero between the interval
`-8<x<-7`

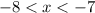
Hence, Option D is not the correct answer.