Question

Jorge is folding a piece of paper to make an origami figure each time he falls the paper the thickness of the paper is double the paper starts out flat with the thickness of 1 millimeter

Answer 1

Part a) see the explanation

Part b) Yes, the relation is an exponential growth function

Explanation:

The complete question is

Jorge is folding a piece of paper to make an origami figure each time he falls the paper the thickness of the paper is double the paper starts out flat with the thickness of 1 millimeter

A. Write a list of six ordered pairs showing the output as the thickness of the paper when the input is the number of times it is folded. Explain how you came up with your ordered pairs.

B. Is this relation a function? Explain why or why not using the ordered pairs you came up with in Part A

Part A) we know that

input value -----> is the number of times you fold it.

output value ----> is its thickness

step 1

When you don't fold it all, the thickness will remain the same, which is 1 mm. The ordered pair would be (0, 1).

step 2

When you fold it once, the thickness will double from 1 mm to 2 mm. The ordered pair would be (1,2).

step 3

When you fold it a second time, the thickness will double from 2 mm to 4 mm. The ordered pair would be (2,4).

step 4

Fold it one more time, and the thickness will be 8 mm. The ordered pair is (3,8)

step 5

Fold it the fourth time, and the thickness doubles. 8 x 2 = 16 mm. The ordered pair is (4, 16)

step 6

Fold it the fifth time, and the thickness goes from 16 mm to 32 mm. The ordered pair is (5,32)

therefore

a list of six ordered pairs are

(0, 1),(1, 2),(2, 4),(3, 8),(4, 16).(5, 32)

Part B)

Let

y ----> thickness of a piece of paper in millimeters

x ---> the the number of times you fold the piece of paper.

we know that

In this problem we have an exponential growth function of the form

`y=a(1+r)^x`

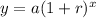
where

a is the initial value

r is the rate of change

we have

`a=1\ mm`

`r=100\%=100/100=1`

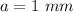
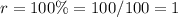
substitute

`y=(1)(1+1)^x`

`y=2^x`

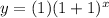
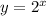
Verify the ordered pairs of Part A)

For x=0 ---->
`y=2^0=1`

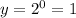
For x=1 ---->
`y=2^1=2`

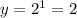
For x=2 ---->
`y=2^2=4`

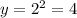
For x=3 ---->
`y=2^3=8`

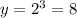
For x=4 ---->
`y=2^4=16`

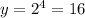
For x=5 ---->
`y=2^5=32`

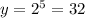
therefore

we have an exponential growth function