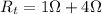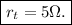Answer:
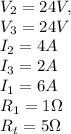
Step-by-step explanation:
The principle of continuity of current demands that
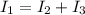 .
.
And applying Kirchhoff's current law two two loops in the circuit, we get:
(1).

and
(2).
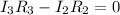 .
.
Since
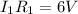 , equation (1) becomes
, equation (1) becomes
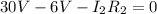

Since

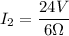

From equation (2) we now get:
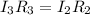
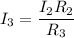

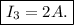
Finally, we solve for
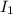
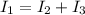
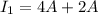
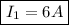
therefore, the resistance
 is
is
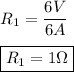
The potential drop
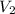 is
is
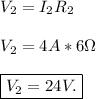
Similarly, the potential drop
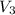 is
is
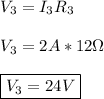
The total resistance of the circuit is
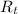
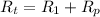
where
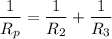
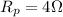 ;
;
therefore,