Ordered pair is

Explanation:
We have the following inequalities:
 and
and
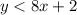 . In order to find ordered pair would be a solution on the graph .Let's solve both inequalities , and will take common solution from both of them !
. In order to find ordered pair would be a solution on the graph .Let's solve both inequalities , and will take common solution from both of them !
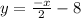 and ,
and ,
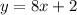 which implies:
which implies:
⇒
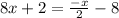
⇒
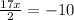
⇒
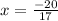
putting value of x in both inequalities we get,
 and
and
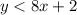
 and
and
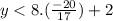
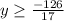 and
and
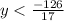
Hence at x =
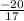 and y =
and y =
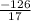 above inequalities are satisfied. ∴ Ordered pair is
above inequalities are satisfied. ∴ Ordered pair is
