Question

There are currently 4000 birds of a particular species in a national park and their number is increasing at a rate of R(t) = 525e0.05t birds/year. If the proportion of birds that survive t years is given by S(t) = e−0.1t, what do you predict the bird population will be 10 years from now? (Round your answer to the nearest whole number.)

Answer 1

It will be 1790.

Explanation:

There are 4000 birds of a particular species in a national park.

Now, the number of birds increasing by the relation
`R(t) = 525 (e)^(0.05t)` birds per year.

So, after 10 years the bird population will become,
`R(10) = 525(e)^(0.05 * 10) = 865.58` plus 4000.

That means the population after 10 years will become (865.58 + 4000) = 4865.58.

Now, the proportion of birds that survive t years is given by
`S(t) = e^(- 0.1t)`.

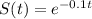So, after 10 years the proportion of birds that survive after 10 years will be

`S(10) = e^(- 0.1 * 10) = 0.368`.

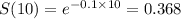Therefore, the predicted population of birds after 10 years from now will be = 4865.58 × 0.368 = 1790. (Answer)