Question

Finallyyy the last one

Answer 1

`\sqrt{(4-8)^(2)+(-3+7)^(2)}`

`4√(2)`

Explanation:

The formula for finding the distance between two lines is:

`d=\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}`

where d is the distance between the points (x₁, y₁) and (x₂, y₂).

By using the distance formula, we can find that the distance between (8, -7) and (4, -3) is:

`d=\sqrt{(4-8)^(2)+(-3+7)^(2)}`

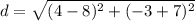
So we know that

`\sqrt{(4-8)^(2)+(-3+7)^(2)}`

is one answers to the question. To find the other answer, if there is one, we will have to evaluate the distance between the two points.

`d=\sqrt{(4-8)^(2)+(-3+7)^(2)}=\sqrt{(-4)^(2)+4^(2)}=√(16+16)=√(32)=4√(2)`

So now we know that

`4√(2)`

is another one of the answers. Since none of the other answer are equal to each other, those are the only two answers.

`\sqrt{(4-8)^(2)+(-3+7)^(2)}`

`4√(2)`

I hope you find this helpful.

Answer 2

B and C

Explanation:

Calculate the distance d using the distance formula

d = √ (x₂ - x₁ )² + (y₂ - y₁ )²

with (x₁, y₁ ) = (8, - 7) and (x₂, y₂ ) = (4, - 3)

d =
`√((4-8)^2+(-3+7)^2)` → B

=
`√((-4)^2+4^2)`

=
`√(16+16)`

=
`√(32)`

=
`√(16(2))`

=
`√(16)` ×
`√(2)`

= 4
`√(2)` → C