Answer:
Step-by-step explanation:
mass of block, m = 2 kg
initial velocity, u = 20 m/s
spring constant, K = 100 N/m
elongation, Δx = 3 - 1 = 2 m
Let v be the velocity when s = 3 m.
Use conservation of energy
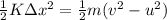
100 x 2 x 2 = 2 x (v² - 400)
200 = v² - 400
v² = 600
v = 24.5 m/s