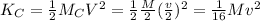Answer:
The rear wagon gains the kinetic energy, but the front wagon will remain at rest.
The two-wagon system will gain a kinetic energy
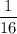 of the kinetic energy gained by the rear wagon.
of the kinetic energy gained by the rear wagon.
Step-by-step explanation:
Let's consider that the masses of the wagons to be 'M'. When the child pushes the rear wagon let's assume that the velocity of the rear wagon be 'v'.
Therefor the kinetic energy gained by the rear wagon be
 .
.
Now let's assume that the velocity of the centre of mass (C), as shown in the figure, be 'V'. So from momentum conservation law we can write,
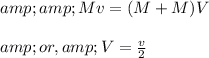
Now the centre of mass (
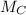 ) is given by
) is given by

So the kinetic energy (
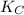 ) of the system will be
) of the system will be