Question

If (−4, 11) and (−6, 5) are the endpoints of a diameter of a circle, what is the equation of the circle?

Answer 1

The equation of the circle is given as:

`(x+5)^2 + (y-8)^2 = 10`

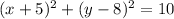
Solution:

Given that,

(−4, 11) and (−6, 5) are the endpoints of a diameter of a circle

The standard form of the equation of a circle is:

`(x-a)^2 + (y-b)^2=r^2`

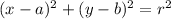
Where,

(a, b) are the co-ordinates of the centre and r is the radius

To find the centre:

Find the midpoint of two given points

`m = ((x_1+x_2)/(2) , (y_1+y_2)/(2))`

`m = ((-4-6)/( 2), (11+5)/(2))\\\\m = (-5, 8)`

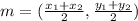
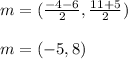
calculate the radius using the distance formula

Distance between center and one end point = radius

(-5, 8) and (-4, 11)

`d = √((x_2-x_1)^2 + (y_2-y_1)^2)`

`d = √((-4+5)^2 + (11-8)^2)\\\\d = √(1 + 9)\\\\d = √(10)`

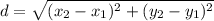
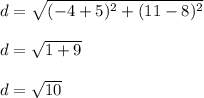
The equation of the circle is given as:

`(x-a)^2 + (y-b)^2=r^2`

`(x+5)^2 + (y-8)^2 = (√(10))^2\\\\(x+5)^2 + (y-8)^2 = 10`

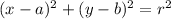
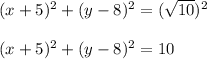
Thus the equation of circle is found