Answer:
a). 0.032
b). 0.999936
c). 0.00768
d). 0.24576
e). 0.9011
f). 0.3446
Explanation:
The given question is incomplete; here is the complete question.
An Olympic archer is able to hit the bull’s-eye 80% of the time. Assume each shot is independent of the others. If she shoots 6 arrows, what’s the probability of each of the following results? a) Her first bull’s-eye comes on the third arrow. b) She misses the bull’s-eye at least once. c) Her first bull’s-eye comes on the fourth or fifth arrow. d) She gets exactly 4 bull’s-eyes. e) She gets at least 4 bull’s-eyes. f) She gets at most 4 bull’s-eyes
a). If archer shots her first bull's-eye on the third arrow.
Since probability to hit the bull's eye = 80% or 0.80
and probability to miss the bull's eye = 20% or 0.20
So P(miss miss hit) = (0.2)(0.2)(0.8) = 0.032
b). She misses the bull's-eye at least one out of 6 arrows.
So, P(misses at least once) = 1 - P(misses all)
=
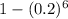
=
![1-[(2)^(6)* (10^(-1))^(6)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/qq2bl19ha7jt7kr5et1j63vh6qj6kc4fmc.png)
=
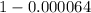
= 0.999936
c). P(4th or 5th) =
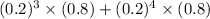
= 0.0064 + 0.00128
= 0.00768
d). For exactly 4 hits,
From the binomial distribution formula,
Binomial probability =
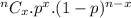
P(exactly 4 hits) =
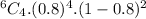
P(exactly 4 hits) = 0.2458
e). She gets at least 4 bull's eyes.
P(x ≥ 4) =

P(x ≥ 4) = 0.9011
f). She gets at most 4 bull's eyes.
P(at most 4 bull's eyes) =
 = 0.3446
= 0.3446