The function f (x) = 2•4^x can be used to represent an exponential growth curve. Which of the following points is NOT on the curve? a. (3,128) b. (2,32) c. (1,8) d. (3,24)

Question

asked Aug 20, 2021 108k views

1 Answer

Lovey · Answer 1 · 2021-08-23T19:42:03+0000

Answer:

d. (3,24)

Explanation:

The given exponential growth curve is

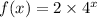
$f(x) = 2 * {4}^(x)$

Any point that does not satisfy the function equation is NOT on the curve.

For (3,128), we substitute x=3, to get:

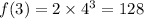
$f(3) = 2 * {4}^(3) = 128$

This point is on the curve.

For (2,32), we substitute x=2,

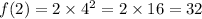
$f(2) = 2 * {4}^(2) = 2 * 16 = 32$

This point is also on this curve.

For (1,8), we have:

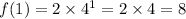
$f(1) = 2 * {4}^(1) = 2 * 4 = 8$

This point is on the curve.

For (3,24), we have:

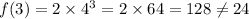
$f(3) = 2 * {4}^(3) = 2 * 64 = 128 \\e24$

This point is NOT on the curve.