Question

A portfolio has a E[r] of 12% and a std deviation of 18%. T-Bills return 7%. What is the maximum level of risk aversion (A) for which the risky portfolio is still preferred to T-Bills? 4.11 3.97 5.04 3.09

Answer 1

The required "option D) 3.09" is correct.

Explanation:

Given,

A portfolio has a E[r] = 12 %, and

A standard deviation (
`\sigma`) = 18 %

We know that,

Specify utility by U = E(r) – 0.5A
`\sigma^2`

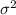
U = 0.12– 0.5(A) ×
`0.18^2`

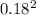
= 0.12 - 0.5 × A × 0.0162

In order for the risky portfolio to be preferred to bills,

The following condition must have:

0.12 – 0.0162A > 0.07

⇒ A <
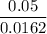`(0.05)/(0.0162)` = 3.09

A must be less than 3.09 for the risky portfolio to be preferred to bills.

Thus, the required "option D) 3.09" is correct.