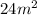Question

a gardener is putting a wire fence along the edge of his garden to keep animals from eating his plants. if he has 20meters of fence, what is the largest rectangular space he can enclose

Answer 1

The largest rectangular space is
`24m^(2)`

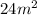
Explanation:

Given a 20m long wire fence, implies that the perimeter of the fence has been given, because Perimeter can be defined as the length of the boundary of a figure (in this case, a rectangle)

So, from the formula: Perimeter = 2 (L + B) =
`20m^(2)`

We have that L + B =
`10m^(2)`

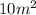
The possible values of L and B are:

(L, B) = (9, 1), (8, 2), (7, 3) and (6, 4).

The areas of the rectangle that will be formed using these values are respectively;
`9m^(2)`,
`16m^(2)`,
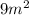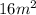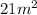`21m^(2)` and
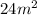`24m^(2)`, the largest area of which is the last which corresponds to the values (6, 4).

The largest rectangular space that the gardener can enclose is therefore
`24m^(2)`