Answer:
The grasshopper will be at 1 foot after 1.50 seconds.
Explanation:
a). A grasshopper jumps straight up with an initial vertical velocity = 8 feet per second
From the equations of vertical motion,
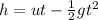
Here h = height of the grasshopper at the time 't'
u = initial velocity
g = Acceleration due to gravity
t = duration or time
Now we plug in the value of initial velocity in this equation.
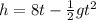
b). In this part we have to calculate the time when the grasshopper is 1 foot off the ground.
from the expression of part (a),
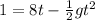
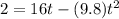
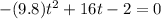
t =

=
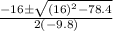
=
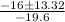
= 1.50, (-0.14) seconds
But the time can not be negative, so the grasshopper will be at 1 foot after 1.50 seconds.