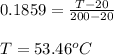Question

A brass rod 175.00 mm long and 5.00 mm in diameter extends horizontally from a casting at 200°C. The rod is in an air environment with [infinity] 20°C and 30 W/m2·K. What is the temperature of the rod 43.75, 87.50, and 175.00 mm from the casting?

Answer 1

(a) for 43.75 mm rod, the temperature is 121.97 ⁰C

(b) for 87.50 mm rod, the temperature is 80.17 ⁰C

(c) for 175.00 mm rod, the temperature is 53.46 ⁰C

Step-by-step explanation:

Given;

L = 175 mm = 0.175 m

D = 5mm = 0.005

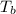`T_b` = 200°C

T∞ = 20°C

Heat transfer coefficient h = 30 W/m²·K

Thermal conductivity of brass K = 133 W/m.°C

`T_X = (T-T_(infinity))/(T_b -T_(infinity))`

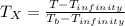
where;

T is the temperature of the rod at different casting distance,

`T_X =(Cosh[m(L-X)]+(h/mk)Sinh[m(L-X)])/(Cosh(mL) +(h/mk)Sinh(mL))`

`m = \sqrt{(4h)/(kD) } = \sqrt{(4*30)/(133*0.005) } = 13.43 m^(-1)\\\\h/mk =(30)/(13.43*133) =0.0168`

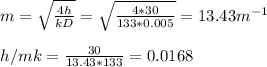
Part (a) for 43.75 mm rod

`T_(43.75) =(Cosh[13.43(0.175-0.04375)] +(0.0168)Sinh[13.43(0.175-0.04375)])/(Cosh(13.43*0.175)+(0.0168)Sinh(13.43*0.175)) \\\\T_(43.75) = (2.9999+0.0475)/(5.2918+0.0875) = 0.5665`

`0.5665 = (T -20)/(200-20) \\\\T =121.97^oC`

Part (b) for 87.50 mm rod

`T_(87.5) =(Cosh[13.43(0.175-0.0875)] +(0.0168)Sinh[13.43(0.175-0.0875)])/(Cosh(13.43*0.175)+(0.0168)Sinh(13.43*0.175)) \\\\T_(87.5) = (1.7735+0.0246)/(5.2918+0.0875) = 0.3343`

`0.3343 = (T -20)/(200-20) \\\\T =80.17^oC`

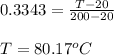
Part (c) for 175.00 mm rod

`T_(175) =(Cosh[13.43(0.175-0.175)] +(0.0168)Sinh[13.43(0.175-0.175)])/(Cosh(13.43*0.175)+(0.0168)Sinh(13.43*0.175)) \\\\T_(175) = (1+0)/(5.2918+0.0875) = 0.1859`

`0.1859 = (T -20)/(200-20) \\\\T =53.46^oC`