Question

An elastic band is hung on a hook and a mass is hung on the lower end of the band. When the mass is pulled down and then released, it vibrates vertically. The equation of motion, s, where s is measured in centimeters and t≥0 in seconds, is given below. (Take the positive direction to be downward.)s = 8 cos (t) + 4 sin (t)I found velocity and accelerationv(t)= -8sin(t) +4cos(t)a(t)= -8cos(t) - 4sin(t)MY problem comes in the question c(c) When does the mass pass through the equilibrium position for the first time?I tired 8 cost + 4 sint =0 getting tan inverse of -8/4. then π+tan inverse of -8/4 which lead me to the answer 1.82?My second problem comes with question dd) How far from its equilibrium position does the mass travel?I don't know how to go about this part of the problem? do I use the the velocity equation set it =0 and then add π?

Answer 1

(c) 2.034 s; (d) 8.944 cm

Explanation:

Velocity and acceleration

s = 8cos(t) + 4sin(t)

v = -8sin(t) + 4cos(t)

a = -8cos(t) + 4sin(t)

(c) Time to first equilibrium position

The equilibrium position is where the mass hangs before it is pulled downward, that is, at s = 0.

Set s = 0 and solve for t.

`\begin{array}{rcl}0 & = & 8\cos t + 4\sin t\\-8\cos t & = & 4\sin t\\-8 & = & 4(\sin t)/(\cos t)\\\\-2 & = & \tan t\\t & = & \arctan(-2)\\& = & -1.107 \pm n\pi\\\end{array}`

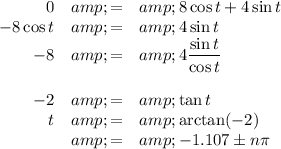
If n = 1,

t = -1.107 + π = 2.034 s

(d) Distance from equilibrium position

The mass will reach its maximum distance when v = 0, that is, when it is at the peak or trough of its oscillation.

Set v = 0 and solve for t.

`\end{array}\begin{array}{rcl}0 & = &- 8\sin t + 4\cos t\\8\sin t & = & 4\cos t\\(\sin t)/(\cos t) & = & (1)/(2)\\\\\tan t & = & 0.5\\t & = & \arctan(0.5)\\& = & 0.4636 \pm n\pi\\\end{array}`

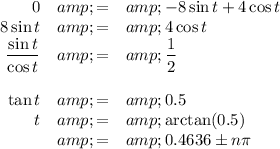
If n = 0,

t = 0.4636

Then

s = 8cos(0.4636) + 4sin(0.4636) = 8×0.8944 + 4×0.4472 = 7.156 + 1.789 = 8.944 cm

The figure below shows the graphs of s and v vs t. They indicate that the mass first reaches its equilibrium position at 2.034 s, and the amplitude of its vibration is 8.944 cm.