2000 is invested at 7% annual interest, compounded monthly. When will the balance triple?

Question

asked Jul 25, 2021 627 views

1 Answer

HTBR · Answer 1 · 2021-07-30T10:48:15+0000

Answer:

15.7 years

Explanation:

Since we were asked how much it would take the principal (2000) to be tripled, we would triple it i.e 2000 × 3 = 6000

To find the time required, t, we would be making use of the equation below

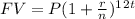
FV = P ( 1 + (r)/(n) ) ^1^2^t

Where FV is the tripled principal

P is the Principal = 2000

r is the percentage Interest = 7% i.e 0.07

n is the number of months that the principal is deposited I.e annually = 12 months

Fixing in the parameters, we have

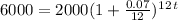
6000 = 2000 (1 + (0.07)/(12) )^1^2^t

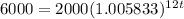
6000 = 2000 (1.005833 )^1^2^t

Dividing both sides of the equality sign would give us

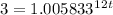
3 = 1.005833^1^2^t

Taking ㏒ of both sides of the equality sign

㏒(
) = ㏒(
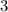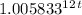1.005833^1^2^t )

㏒(
) = (
12t ) (㏒
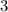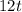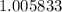1.005833 )

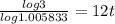
(log 3)/(log 1.005833) = 12t

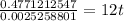
(0.4771212547)/(0.0025258801) = 12t

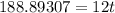
188.89307 = 12t

Therefore
= 15.7 years