Answer: The value of equilibrium constant for the given reaction is 99.85
Step-by-step explanation:
To calculate the number of moles for given molarity, we use the equation:
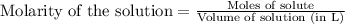 .....(1)
.....(1)
- For
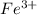 ions:
ions:
Molarity of
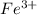 solution =
solution =
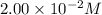
Volume of solution = 7.00 mL = 0.007 L (Conversion factor: 1 L = 1000 mL)
Putting values in equation 1, we get:
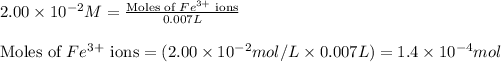
- For
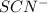 ions:
ions:
Molarity of
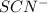 solution =
solution =
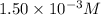
Volume of solution = 2.00 mL = 0.002 L
Putting values in equation 1, we get:
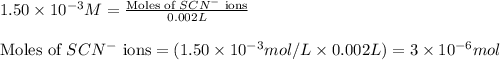
Volume of the container = [7 + 2 + 1] = 10 mL = 0.010 L
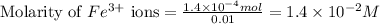
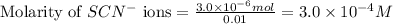
The chemical equation for the formation of
![[FeSCN^(2+)]](https://img.qammunity.org/2021/formulas/chemistry/college/3el1locn9l81fse9abfgsi695utza8p7sd.png) complex follows:
complex follows:
![Fe^(2+)+SCN^-\rightleftharpoons [FeSCN^(2+)]](https://img.qammunity.org/2021/formulas/chemistry/college/s7tjosg3lnsebon94qwbc1waam3cvdicwg.png)
Initial: 0.014
At eqllm: 0.014-x
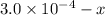 x
x
We are given:
Equilibrium concentration of
![[FeSCN^(2+)]=1.74* 10^(-4)M=x](https://img.qammunity.org/2021/formulas/chemistry/college/fhybgtkpd7zhpr1alumwkb0efbsyj7wj8e.png)
Equilibrium concentration of
![[Fe^(2+)]\text{ ions}=(1.4* 10^(-2)-x)=(1.4-0.0174)* 10^(-3)=1.383* 10^(-2)M](https://img.qammunity.org/2021/formulas/chemistry/college/ecxxp7ee15qik8evilk6dx8bhittesr1f2.png)
Equilibrium concentration of
![[SCN^(-)]\text{ ions}=(3.0* 10^(-4)-x)=(3.0-1.74)* 10^(-4)=1.26* 10^(-4)M](https://img.qammunity.org/2021/formulas/chemistry/college/icsagtu323q2y52cg2imbsty5q8ugcyhfg.png)
The expression of
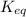 for above equation follows:
for above equation follows:
![K_(eq)=([FeSCN^(2+)])/([Fe^(3+)][SCN^-])](https://img.qammunity.org/2021/formulas/chemistry/college/f0rx3j4nhx33v02eizd15kjmhkm8naf1db.png)
Putting values in above equation, we get:
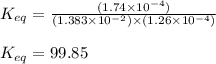
Hence, the value of equilibrium constant for the given reaction is 99.85