Question

Ying is a professional deep water free diver.

His altitude (in meters relative to sea level), xxx seconds after diving, is modeled by:

D(x) 1/36(x-60)^2-100
How many seconds after diving will Ying reach his lowest altitude?

Answer 1

60 seconds

Explanation:

In this problem, the altitude of Ying at time x is given by the equation

`D(x)=(1)/(36)(x-60)^2-100`

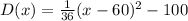
where

x is the time in seconds

D is the altitude above sea level, in meters

Here we want to find the time x' at which Ying reach his lowest altitude. This means that we have to find the minimum of the function D(x). In order to do that, first we rewrite the function as

`D(x)=(1)/(36)(x^2-120x+3600)-100\\D(x)=(1)/(36)x^2-(10)/(3)x+100-100\\D(x)=(1)/(36)x^2-(10)/(3)x`

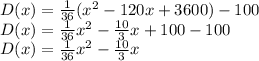
This is an upward parabola, written in the form:

`y=ax^2+bx+c`

We know that the minimum of an upward parabola corresponds to its vertex, which has x-coordinate of

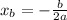`x_b=-(b)/(2a)` (1)

In this case,

`b=-(10)/(3)\\a=(1)/(36)`

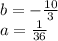
Substituting into (1), we find

`x_b=-(-10/3)/(2(1/36))=(10)/(3)\cdot 18 =60`

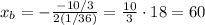
So, the minimum of D(x) occurs at x = 60: therefore, Ying reaches his lowest altitude after 60 seconds.