Answer:
7.602729%
Step-by-step explanation:
Given:
Rate of interest = 7.35% = 7.35/100 = 0.0735
Effective Annual Rate (Monthly) = ?
Rate of interest(monthly) = 0.0735 / 12 = 0.006125
n = 1 year x 12 = 12 month
Computation:
Effective Annual Rate (Monthly) =
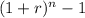
Effective Annual Rate (Monthly) =
![[ (1 + 0.006125 )^(12) - 1 ] * 100 \\](https://img.qammunity.org/2021/formulas/business/high-school/phzvg95o0no7nhx8ltxlhd1o13kiu3faez.png)
![[ (1 .006125 )^(12) - 1 ] * 100 \\[ 1.07602729 - 1 ] * 100\\ [0.07602729 ] * 100 \\7.602729](https://img.qammunity.org/2021/formulas/business/high-school/wtblf01l91zcnxzt5r19f4930miw5t27va.png)
Effective Annual Rate (Monthly) = 7.602729%