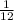Question

Solve: Mike rolls two number cubes. What is the probability that the sum of the two number will be less than 4?

Answer 1

The probability that the sum of the two number will be less than 4 is
`(1)/(12)`

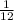
Step-by-step explanation:

It is given that Mike rolls two number cubes.

It is given by the sample space S.

Let A be the event that the sum of the two number will be less than 4.

The sample space is given by

`S=\left\{\begin{array}{l}(1,1),(1,2),(1,3),(1,4),(1,5),(1,6) \\(2,1),(2,2),(2,3),(2,4),(2,5),(2,6) \\(3,1),(3,2),(3,3),(3,4),(3,5),(3,6) \\(4,1),(4,2),(4,3),(4,4),(4,5),(4,6) \\(5,1),(5,2),(5,3),(5,4),(5,5),(5,6) \\(6,1),(6,2),(6,3),(6,4),(6,5),(6,5)\end{array}\right.`

Hence, the total probability of the sample space is
`P(S)=36`

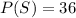
To determine the probability of the sum of the two number will be less than 4, we need to add the outcomes of the two numbered cubes which results in the value less than 4.

Thus, we get,

`A=(1,1),(1,2),(2,1)`

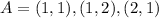
Thus,

`P(A)=3`

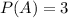
The probability that the sum of the two number will be less than 4 is given by

`(P(A))/(P(S)) =(3)/(36)`

`(P(A))/(P(S)) =(1)/(12)`

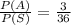
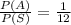
Thus, the probability that the sum of the two number will be less than 4 is
`(1)/(12)`