Question

On a piece of paper, use a protractor to construct right triangle ABC with AB=3 in. , m∠A=90° , and m∠B=45° .

What statement is true about the triangle?

AC=3 in.

BC=3 in.

BC=6 in.

AC=6 in.

Answer 1

Option A:
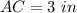`$A C=3 \ in` is true about the triangle.

Step-by-step explanation:

The measurements of the right triangle ABC is
`A B=3 \ in` ,
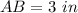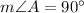`m \angle A=90^(\circ)` and
`\mathrm{m} \angle{B}=45^(\circ)`

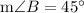
The image of the triangle having these measurements is attached below:

Option A:
`$A C=3 \ in`

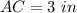
Using Pythagorean theorem, we have,

`tan \ 45^(\circ)= (AC)/(3)`

`1* 3= AC`

`3=AC`

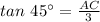
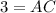
Thus, the length of AC is
`$A C=3 \ in`

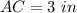
Therefore, Option A is true about the triangle.

Hence, Option A is the correct answer.

Option B:
`$B C=3\ in`

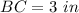
Using Pythagorean theorem, we have,

`cos \ 45^(\circ)=(3)/(BC)`

`BC=(3)/(cos \ 45^(\circ))`

`BC=(3)/(0.707)`

`BC=4.24`

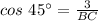
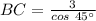
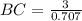
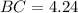
Thus, the length of BC is
`BC=4.24 \ in`

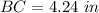
Therefore, Option B is not true about the triangle.

Hence, Option B is not the correct answer.

Option C:
`$B C=6\ in`

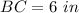
Using Pythagorean theorem, we have,

`cos \ 45^(\circ)=(3)/(BC)`

`BC=(3)/(cos \ 45^(\circ))`

`BC=(3)/(0.707)`

`BC=4.24`

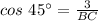
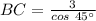
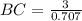
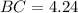
Thus, the length of BC is
`BC=4.24 \ in`

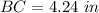
Therefore, Option C is not true about the triangle.

Hence, Option C is not the correct answer.

Option D:
`$A C=6\ in`

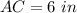
Using Pythagorean theorem, we have,

`tan \ 45^(\circ)= (AC)/(3)`

`1* 3= AC`

`3=AC`

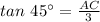
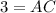
Thus, the length of AC is
`$A C=3 \ in`

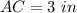
Therefore, Option D is not true about the triangle.

Hence, Option D is not the correct answer.