Question

Y varies jointly as x and z, and inversely as w: y=3 when x=-2, z=6, and w=12.

•Write the equation that represents this relationship.
•What is the constant?

Answer 1

Write the equation that represents this relationship

`y = -3 * (xz)/(w)`

The constant is -3

Solution:

Given that,

y varies jointly as x and z, and inversely as w

Therefore,

`y \propto (xz)/(w)`

`y = k * (xz)/(w) ------ eqn\ 1`

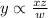
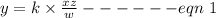
Where, k is constant of propotionality

y = 3 when x = -2, z = 6, and w = 12

Substitute in eqn 1

`3 = k * (-2 * 6)/(12)\\\\3 = k * -1\\\\k = -3`

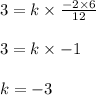
Write the equation that represents this relationship

Substitute k = -3 in eqn 1

`y = -3 * (xz)/(w)`

Thus the equation is found