Question

19. The marked price of an oven is 30% above its cost. In a sale, it is

sold at a discount of 25% on its marked price and the discount is
$221.
(a) Find the marked price and the cost of the oven.
(b) Find the percentage loss.
Example 6.21

Answer 1

a) Marked price: $884, Cost: $680

b) 2.5 %

Explanation:

a)

Let's call:

P = marked price of the oven

C = cost of the oven

We know that:

- The marked price of the oven is 30% above the cost, which means

`P=(1+(30)/(100))C=1.30C` (1)

- In the sale, the oven is sold at a discount of 25% on its marked price; so the price of the sale is (we call it S)

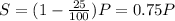`S=(1-(25)/(100))P=0.75P` (2)

- We also know that the discount, which is the difference between the makerd price (P) and the discounted price (S) is

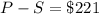`P-S=\$221` (3)

Substituting (2) into (3) we find marked price

`P-0.75P=\$221\\0.25P=\$221\\P=(221)/(0.25)=\$884`

Therefore, the cost of the oven is (from eq(1)):

`C=(P)/(1.30)=(884)/(1.30)=\$680`

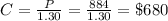
b)

The percentage loss in this situation is given by the difference between cost of the oven and the final price at which the oven is sold.

In this case, we have:

C = $680 (cost of the oven)

The discounted prices is S, and can be f ound using eq(3):

`S=P-221=884-221=\$663`

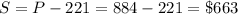
Therefore, the oven costs 680$ but it is sold at 663$.

Therefore, we can calculate the percentage loss using the equation:

`Loss=(C-S)/(C)\cdot 100 = (680-663)/(680)\cdot 100 =0.025\cdot 100 = 2.5\%`

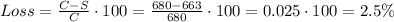
So, a percentage loss of 2.5%.