Question

Question 3

The function H(t) = -161 64t 12 shows the height (t), in feet, of a baseball after t seconds. A second baseball moves in the air along a path represented by g(t) = 10 10.41, where 90 is the height, in feet, of the object from the ground at time t seconds.

Part A: Create a table using integers 1 through 4 for the 2 functions Between what 2 seconds is the solution to H(t) = g0) located? How do you know?

Part B: Explain what the solution from Part A means in the context of the problem.

Answer 1

• Part A: Between t = 3 seconds and t = 4 seconds.

• Part B: the solution is the moment when the two baseballs have the same height.

Step-by-step explanation:

The functions are garbled. The correct functions are:

`H(t)=-16t^2+64t+12`

`g(t)=10+10.41t`

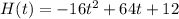
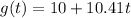
Part A: Create a table using integers 1 through 4 for the 2 functions Between what 2 seconds is the solution to H(t) = g(t) located? How do you know?

Table:

t(s) H(t) = -16t² + 64t + 12 g(t) = 10 + 1.4t

1 -16(1)² + 64(1) + 12 = 60 10 + 1.4(1) = 11.4

2 -16(2)² + 64(2) + 12 = 76 10 + 1.4(2) = 12.8

3 -16(3)² + 64(3) + 12 = 60 10 + 1.4(3) = 14.2

4 -16(4)² + 64(4) + 12 = 12 10 + 1.4(4) = 15.6

The solution is between t = 3 s and t = 4 s.

You know it because the two functions are continuous, and at t = 3 seconds H(t) is greater than g(t), while at t = 4 seconds H(t) is greater than g(t). Thus, necessarily at one instant between t = 3 seconds and t = 4 seconds the two functions have the same value.

Part B: Explain what the solution from Part A means in the context of the problem.

The solution is the point of intersection of the graphs. Since each graph is the path of a ball, the point of intersection is when the two paths intersect.

Then the solutions means that the two baseballs are at the same height at a time between t = 3 seconds and t = 4 seconds.

You cannot assure that the two balls collide with each other because the function only shows height, but not the other coordinates in the space.