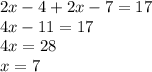1. ∠LMN = 167°
2.

3. ∠LMT = 96 + x = 96 - 1 = 95°
4.
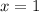
5.
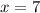
Step-by-step explanation:
1.
We have ∠TMN = 144° & ∠LMT = 23° and we need to find ∠LMN which is sum of angles TMN & LMT ∴ ∠LMN = ∠TMN + ∠LMT = 144° + 23° = 167°
2.
We have , ∠GHI = 173° , ∠GHQ= 29 + x , ∠QHI = 162
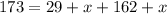 + x, in order to find x we see in question that ∠GHI is sum of angles ∠QHI & ∠GHQ i.e.
+ x, in order to find x we see in question that ∠GHI is sum of angles ∠QHI & ∠GHQ i.e.
⇒
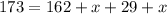
⇒

⇒

3.
We have, ∠TMN = x + 72 , ∠LMN = 166°, ∠LMT = 96 + x. Here we know that ∠LMN is sum of angles ∠TMN & ∠LMT i.e.
⇒
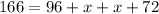
⇒
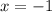
∴ ∠LMT = 96 + x = 96 - 1 = 95°
4.
To find length we have line PR = 7 + x & line Q = 8 ∴
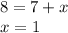
5.
We have ,