Answer:
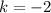
Explanation:
Given matrix
![A=\left[\begin{array}{ccc}4&2\\-1&2\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/ihwmmo9xfw2ktecawsyue45qcsprdal1x9.png)
And
![B=\left[\begin{array}{ccc}2&4\\-2&k\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/rkg3yuqd4y7ahcaha3pyhyulwss1cfxao5.png)
We need to find the value of
 , that will make
, that will make
 .
.
Let us find
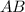
![AB=\left[\begin{array}{ccc}4&2\\-1&2\end{array}\right]* \left[\begin{array}{ccc}2&4\\-2&k\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/nuwyjm0jukb5cvmeak8qt761qrywml3o1i.png)
![AB=\left[\begin{array}{ccc}4&16+2k\\-6&-4+2k\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/nsopc8frm6co8qdl6htkztp1a6g9o1j1m0.png)
Now, let us find
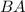
![BA=\left[\begin{array}{ccc}2&4\\-2&k\end{array}\right]* \left[\begin{array}{ccc}4&2\\-1&2\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/f92vlfef9648v4tlu196sgzhym1lls1dbx.png)
![BA=\left[\begin{array}{ccc}4&12\\-8-k&-4+2k\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/mihlymox49tmyno8o2to8e1l4zx969e031.png)
Put

![\left[\begin{array}{ccc}4&16+2k\\-6&-4+2k\end{array}\right]=\left[\begin{array}{ccc}4&12\\-8-k&-4+2k\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/r6lu9h6vxe72qa8f7l4x5nwz4z92789qm7.png)
In order to make
 , the
, the
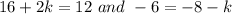 should be equal. As other two values are equal that are
should be equal. As other two values are equal that are
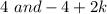
By solving each equation
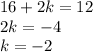
And
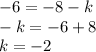
We can see if the value
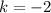 then
then
