Find the minimum sample size necessary to be 99% confident that the population mean is within 3 units of the sample mean given that the population standard deviation is 29.

Question

asked Nov 24, 2021 224k views

1 Answer

Vbp · Answer 1 · 2021-12-01T04:36:22+0000

Answer:

The minimum sample size required is 207.

Explanation:

The (1 - α) % confidence interval for population mean μ is:

$CI=\bar x\pm z_(\alpha /2)(\sigma)/(√(n))$

The margin of error of this confidence interval is:

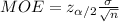
$MOE=z_(\alpha /2)(\sigma)/(√(n))$

Given:

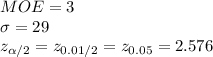
$MOE=3\\\sigma=29\\z_(\alpha /2)=z_(0.01/2)=z_(0.05)=2.576$

*Use a z-table for the critical value.

Compute the value of n as follows:

$MOE=z_(\alpha /2)(\sigma)/(√(n))\\3=2.576* (29)/(√(n)) \\n=[(2.576*29)/(3) ]^(2)\\=206.69\\\approx207$

Thus, the minimum sample size required is 207.