Question

The bearing of a lighthouse from a ship is N 37° E. The ship sails 2.5 miles further from the lighthouse. The new bearing is 25°E. What is the distance between the lighthouse and ship at the new location?

Answer 1

The distance between the ship at N 25°E and the lighthouse would be 7.26 miles.

Explanation:

The question is incomplete. The complete question should be

The bearing of a lighthouse from a ship is N 37° E. The ship sails 2.5 miles further towards the south. The new bearing is N 25°E. What is the distance between the lighthouse and the ship at the new location?

Given the initial bearing of a lighthouse from the ship is N 37° E. So,
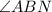`\angle ABN` is 37°. We can see from the diagram that
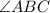`\angle ABC` would be
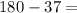`180-37=` 143°.

Also, the new bearing is N 25°E. So,
`\angle BCA` would be 25°.

Now we can find
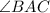`\angle BAC`. As the sum of the internal angle of a triangle is 180°.

`\angle ABC+\angle BCA+\angle BAC=180\\143+25+\angle BAC=180\\\angle BAC=180-143-25\\\angle BAC=12`

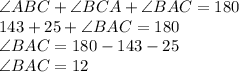
Also, it was given that ship sails 2.5 miles from N 37° E to N 25°E. We can see from the diagram that this distance would be our BC.

And let us assume the distance between the lighthouse and the ship at N 25°E is
`AC=x`

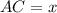
We can apply the sine rule now.

`(x)/(sin(143))=(2.5)/(sin(12))\\ \\x=(2.5)/(sin(12))* sin(143)\\\\x=(2.5)/(0.207)* 0.601\\ \\x=7.26\ miles`

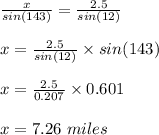
So, the distance between the ship at N 25°E and the lighthouse is 7.26 miles.