Question

Which region in the graph below is the solution of the system of inequalities given below?

Answer 1

Option C: Region 2 is the solution to the system of inequalities

Step-by-step explanation:

The system of inequalities is
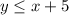`y \leq x+5` and
`y \geq-x-8`

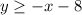
Let us substitute the coordinate
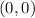`(0,0)` in the inequality
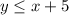`y \leq x+5` , we get,

`0\leq 0+5`

`0\leq 5`

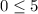
Hence, the inequality becomes true.

So, let us shade the region that contains the point
`(0,0)`

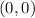
And hence the shaded portion comes under the region 2 and region 3.

Now, let us substitute the coordinate
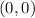`(0,0)` in the inequality
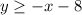`y \geq-x-8`, we get,

`0\geq 0-8`

`0\geq -8`

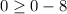
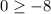
Hence, the inequality becomes true.

So, let us shade the half that contains the point
`(0,0)`

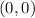
And hence the shaded portion comes under the region 1 and region 2.

The solution of the system of inequalities is the intersection of the regions of the two inequalities.

Hence, the two inequalities intersect at the region 2.

Therefore, Region 2 is the solution to the system of inequalities.

Thus, Option C is the correct answer.