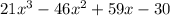The solution is
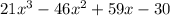
Step-by-step explanation:
The given expression is
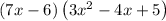
We need to multiply and simplify the expression.
Let us multiply each of term within the parenthesis.
Thus, we get,
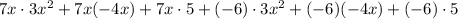
Now, simplifying each term in the expression, we have,
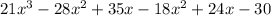
Adding the like terms, we get,
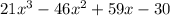
Hence, the simplified expression is
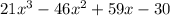
Therefore, the solution is