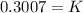Question

Over this period, the population grew roughly exponentially. Taking t = 0 to correspond to the start of the year 1790, we can approximate the population size by the exponential curve N(t) = N0 ekt for some N0 and k. Find the best fitting values of N0 and k by taking natural logs of the population sizes and using linear regression. (Give your answers correct to at least four decimal places, but be careful to use the unrounded values when you calculate the answers to the last two parts of this problem!)

Answer 1

`N_0=3.929`

`K=0.3007`

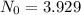
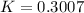
Explanation:

This question is incomplete. I have attached a complimentary image of the census which captures the number of inhabitants of the U.S over the period 1790 to 1850. The data captured in this attachment completes the question.

From the question, it is given that

`N(t) = N_0e^(kt)`

where
`N_0` and
`K` are constant

Note that

`t=0`
`for`
`1790`

`t=1`
`for`
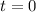
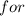
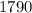
`1800` and so it goes on ...

Therefore, for the year 1790,

`N(t)=N_0e^(kt)\\3.929=N_0e^(k(0))=N_0e^0\\3.929=N_0`

And for the year 1800,

`5.308=N_0e^(k(1))\\5.308=3.292e^k\\(5.308)/(3.929) =e^k`

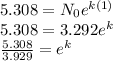
Taking the natural log on both sides, we get

`ln(1.3509)=lne^k\\0.3007=Klne\\`

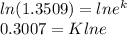
where
`lne = 1`

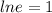
equation becomes,

`0.3007=K`