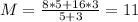Question

One sample has a mean of and a second sample has a mean of . The two samples are combined into a single set of scores. What is the mean for the combined set if both of the original samples have scores

Answer 1

a) For this case we can use the definition of weighted average given by:

`M = ( \bar X_1 n_1 + \bar X_2 n_2)/(n_1 +n_2)`

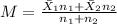
And if we replace the values given we have:

`M = (8*4 + 16*4)/(4+4)= 12`

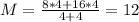
b)
`M = (8*3 + 16*5)/(3+5)= 13`

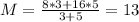
c)
`M = (8*5 + 16*3)/(5+3)= 11`

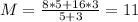
Explanation:

Assuming the following question: "One sample has a mean of M=8 and a second sample has a mean of M=16 . The two samples are combined into a single set of scores.

a) What is the mean for the combined set if both of the original samples have n=4 scores "

For this case we can use the definition of weighted average given by:

`M = ( \bar X_1 n_1 + \bar X_2 n_2)/(n_1 +n_2)`

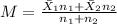
And if we replace the values given we have:

`M = (8*4 + 16*4)/(4+4)= 12`

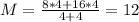
b) what is the mean for the combined set if the first sample has n=3 and the second sample has n=5

Using the definition we have:

`M = (8*3 + 16*5)/(3+5)= 13`

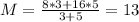
c) what is the mean for the combined set if the first sample has n=5 and the second sample has n=3

Using the definition we have:

`M = (8*5 + 16*3)/(5+3)= 11`