Question

Let’s say that you take out a loan in the amount of $100,000. You plan to set aside $1,450 of your monthly profits for the next 10 years to repay the loan. After 10 years have passed, you will make a lump-sum payment with that money to clear the loan. What is the maximum interest rate that you should agree to in order to accomplish this? How did you arrive at your answer?

Answer 1

Maximum Interest rate R≈0.06167 ≈0.6167 %

Step-by-step explanation:

Answer:

Step-by-step explanation:

Let: P be the loan amount(P=$100000), R be rate(R=?), I be interest after 10yrs(I=?), T to be time to repay (t=10yrs 12=12months: since a certain amount is set up on a monthly bases for the purpose of payment, we assume a monthly rate)

To get the interest I paid at the end of 10yrs, do the following:

let total lump sum repayable be TL

∵TL=$1450x12monthsx10yrs=$174000

Hence,

I=$174000-$100000=$74000

Using R=
`(I)/(PT)`

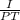
where I=$74000, P=$100000 and T=10*12=120months

R=
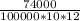`(74000)/(100000*10*12)`=0.006167

R≈0.006167

multiplying R by 100, we have R in percentage as,

R≈0.6167 % Interest rate