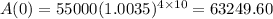Answer:
(a)

(b) At t = 0, A = 55,000
At t = 4, A = 58,162.19
At t = 7, A = 60,652.57
At t = 10, A = 63,249.60
Explanation:
(a) The amount on a compound interest is given by
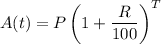
P is the principal invested, R is the rate and T is the time.
The principal is 55,000. With the interest compounded quarterly, there are four compundings in a year. Hence each year will have four periods.
The function for the amount is then
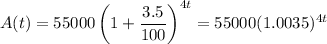
(b)
At t = 0,
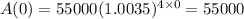
At t = 4,
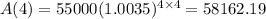
At t = 7,
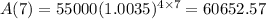
At t = 10,