The given question is incomplete. The complete question is as follows.
A box of oranges which weighs 83 N is being pushed across a horizontal floor. As it moves, it is slowing at a constant rate of 0.90 m/s each second. The push force has a horizontal component of 20 N and a vertical component of 25 N downward. Calculate the coefficient of kinetic friction between the box and the floor.
Step-by-step explanation:
The given data is as follows.
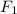 = 20 N,
= 20 N,
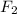 = 25 N, a = -0.9
= 25 N, a = -0.9
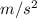
W = 83 N
m =

= 8.46
Now, we will balance the forces along the y-component as follows.
N = W +
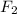
= 83 + 25 = 108 N
Now, balancing the forces along the x component as follows.
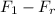 = ma
= ma
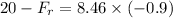
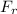 = 7.614 N
= 7.614 N
Also, we know that relation between force and coefficient of friction is as follows.
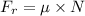

=
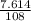
= 0.0705
Thus, we can conclude that the coefficient of kinetic friction between the box and the floor is 0.0705.