Answer:
(a)
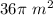
(b)
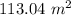
Explanation:
(a) Write and simplify an expression for the exact area of the sidewalk.
(b) Find the approximate area of the sidewalk. Use 3.14 to approximate .
(a) The sidewalk area is the difference in the area of outer circle and inner circle.
Use formula
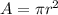 for the area of the circle:
for the area of the circle:
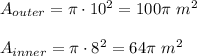
The difference is
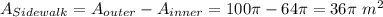
(b) Use approximation
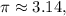 then
then
