Question

Solid vanadium crystallizes in a body-centered cubic structure and has a density of 6.00 g/cm3. First determine the number of atoms of vanadium in a unit cell. Then, calculate the atomic radius of vanadium.

Answer 1

The given question is incomplete. The complete question is as follows.

Solid vanadium crystallizes in a body-centered cubic structure and has a density of 6.00 g/cm3. Assuming the vanadium atomic radius is 132 pm, is the vanadium unit cell primitive cubic, body centered cubic, or face centered cubic.

Step-by-step explanation:

The given data is as follows.

Density = 6.00
`g/cm^(3)`

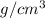
radius = 132 pm

Relation between edge length and volume is as follows.

a = ∛V

= ∛No. of atoms

=
`\sqrt[3]{(mass)/(density * N_(A))}`

=
`\sqrt[3]{(50.941 g/mol)/(6.0 g/cm^(3) * 6.022 * 10^(23))}`

= 2.4 ∛No. of atoms

So, there will be three possibilities which are as follows.

• SC, 1 atom and r =
  `(a)/(2)`

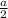
Here, a = 2.4, and r = 1.2
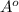`A^(o)` which is not right.

• For BCC, there are two atoms and r =
  `(√(3)a)/(4)`

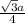
So, a =
`1.26 * 2.4`

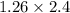
= 3.02 and, r = 1.31
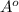`A^(o)` which is a good fit to the measured radius.

• For FCC, there are 4 atoms and r =
  `(√(2)a)/(4)`

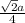
So, a =
`1.59 * 2.4`

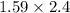
= 3.81 and r = 1.35
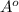`A^(o)` which will not fit to the measured radius as well as BCC.