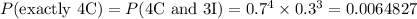Question

Each of the 7 members of a judge panel independently makes a correct decision with prob-ability 0.7. If the panel’s decision is made by majority rule, what is the probability that the panel makesthe correct decision? Given that exactly 4 of the judges agreed, what is the probability that the panelmade the correct decision?

Answer 1

(a) 0.139258

(b) 0.0064827

Explanation:

Let the probability that each member makes a correct decision be
`p` and the probability that each member makes an incorrect decision be
`q`.

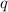From the question,
`p = 0.7`

p and q are mutually exclusive. Hence,

`p+q = 1`

`q = 1 - p=1-0.7 = 0.3`

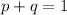
(a) For majority rule, it means at least 4 members decisions are taken. Taking "C" to mean "correct" and "I" to mean "incorrect", we could have 4C against 3I, 5C against 2I, 6C against 1I and 7C against 0I.

The probability of the correct decision being made is

`P(\ge\text{4C}) = P(\text{4C and 3I}) + P(\text{5C and 2I}) +P(\text{6C and 1I}) +P(\text{7C and 0I})`

`P(\ge\text{4C}) = (0.7^4*0.3^3)+(0.7^5*0.3^2)+(0.7^6*0.3^1)+(0.7^7*0.3^0)`

`P(\ge\text{4C}) = 0.0064827 + 0.0151263 + 0.0352947 + 0.0823543 = 0.139258`

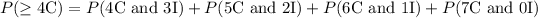
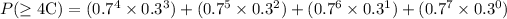
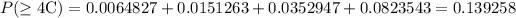
(b)
`P(\text{exactly 4C}) = P(\text{4C and 3I}) = 0.7^4*0.3^3 = 0.0064827`